- Подробности
- Категория: Серия учебников "Математика в техническом университете"
Перейти к списку | Аннотация | Содержание
 Аннотация
Аннотация
Книга является шестым выпуском комплекса учебников «Математика в техническом университете». Знакомит читателя с понятиями неопределенного и определенного интегралов и методами их вычисления. Уделено внимание приложениям определенного интеграла, приведены примеры и задачи физического, механического и технического содержания.
Содержание учебника соответствует курсу лекций, который автор читает в МГТУ им. Н.Э. Баумана.
Для студентов технических университетов. Может быть полезен преподавателям и аспирантам.
Содержание
| Предисловие | ||
| Основные обозначения | ||
| 1. | Неопределенный интеграл | |
| 1.1. | Вводные замечания | |
| 1.2. | Понятия первообразной и неопределенного интеграла | |
| 1.3. | Свойства неопределенного интеграла | |
| 1.4. | Основные неопределенные интегралы | |
| 1.5. | Интегрирование подстановкой и заменой переменного | |
| 1.6. | Интегрирование по частям | |
| Д.1.1. | Первообразная непрерывной функции | |
| Вопросы и задачи | ||
| 2. | Интегрирование рациональных дробей | |
| 2.1. | Дробно-рациональные подынтегральные функции | |
| 2.2. | Интегралы от простейших рациональных дробей | |
| 2.3. | Разложение правильной рациональной дроби на простейшие | |
| 2.4. | Интегрирование дробно-рациональных функций | |
| Д.2.1. | Метод Остроградского | |
| Д.2.2. | Интегрирование рациональных функций, содержащих биномы | |
| Вопросы и задачи | ||
| 3. | Интегрирование иррациональных выражений | |
| 3.1. | Рациональные функции от радикалов | |
| 3.2. | Интегрирование функций, содержащих радикалы от дробно-линейной функции | |
| 3.3. | Подстановки Эйлера | |
| 3.4. | Другие приемы интегрирования | |
| 3.5. | Тригонометрические и гиперболические подстановки | |
| 3.6. | Интегралы от дифференциального бинома | |
| Д.3.1. | Геометрический смысл подстановок Эйлера | |
| Д.3.2. |
Об интегрировании функций вида 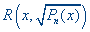 |
|
| Вопросы и задачи | ||
| 4. | Интегралы от некоторых трансцендентных функций | |
| 4.1. | Рациональные функции синуса и косинуса | |
| 4.2. | Рациональные степени синуса и косинуса | |
| 4.3. | Экспоненциальные и гиперболические функции | |
| 4.4. | Различные трансцендентные выражения | |
| Вопросы и задачи | ||
| 5. | Интеграл Ньютона | |
| 5.1. | Понятие определенного интеграла Ньютона | |
| 5.2. | Формула Ньютона - Лейбница | |
| 5.3. | Свойства интеграла Ньютона | |
| 5.4. | Теорема о среднем значении и ее следствия | |
| 5.5. | Интеграл Ньютона с переменными пределами | |
| 5.6. | Геометрическая и механическая интерпретации интеграла Ньютона | |
| 5.7. | Способы вычисления интеграла Ньютона | |
| Вопросы и задачи | ||
| 6. | Определенный интеграл | |
| 6.1. | Интегральная сумма и ее предел | |
| 6.2. | Интеграл Римана | |
| 6.3. | Суммы и интегралы Дарбу | |
| 6.4. | Критерий существования определенного интеграла | |
| 6.5. | Классы интегрируемых функций | |
| 6.6. | Свойства интегрируемых функций | |
| 6.7. | Основные свойства определенного интеграла | |
| 6.8. | Теоремы о среднем значении для определенного интеграла | |
| 6.9. | Определенный интеграл с переменным пределом | |
| 6.10. | Вычисление определенного интеграла | |
| Д.6.1. | Доказательство теорем о классах интегрируемых функций | |
| Д.6.2. | Доказательство теорем 6.19 и 6.20 | |
| Д.6.3. | Связь интегралов Ньютона и Римана | |
| Д.6.4. | Обобщение теорем о среднем значении | |
| Вопросы и задачи | ||
| 7. | Несобственные интегралы | |
| 7.1. | Интегралы по бесконечному промежутку | |
| 7.2. | Основные свойства сходящихся несобственных интегралов по бесконечному промежутку | |
| 7.3. | Признаки сходимости интегралов по бесконечному промежутку | |
| 7.4. | Интегралы от неограниченных функций | |
| 7.5. | Сходимость интегралов от неограниченных функций | |
| 7.6. | Абсолютная и условная сходимость несобственных интегралов | |
| 7.7. | Другие признаки сходимости несобственных интегралов | |
| 7.8. | Примеры исследования несобственных интегралов на сходимость | |
| 7.9. | Преобразование несобственных интегралов | |
| 7.10. | Главные значения несобственных интегралов | |
| Вопросы и задачи | ||
| 8. | Интегралы, зависящие от параметра | |
| 8.1. | Определенные интегралы, зависящие от параметра | |
| 8.2. | Дифференцирование интегралов по параметру | |
| 8.3. | Интегрирование по параметру | |
| 8.4. | Равномерная сходимость несобственных интегралов | |
| 8.5. | Признаки равномерной сходимости несобственных интегралов | |
| 8.6. | Непрерывность и дифференцируемость несобственных интегралов по параметру | |
| 8.7. | Интегрирование несобственных интегралов по параметру | |
| 8.8. | Эйлеровы интегралы | |
| Вопросы и задачи | ||
| 9. | Приложения определенного интеграла | |
| 9.1. | Общая схема применения интеграла | |
| 9.2. | Длина кривой | |
| 9.3. | Площадь плоской фигуры | |
| 9.4. | Объем тела | |
| 9.5. | Площадь поверхности | |
| 9.6. | Вычисление масс и моментов инерции | |
| 9.7. | Статические моменты и координаты центра масс | |
| 9.8. | Работа, энергия, сила давления | |
| Д.9.1. | Движение материальной точки в центральном поле тяготения | |
| Вопросы и задачи | ||
| 10. Численное интегрирование | ||
| 10.1. | Существо подхода к численному интегрированию | |
| 10.2. | Формула трапеций | |
| 10.3. | Формула парабол | |
| 10.4. | Формулы прямоугольников | |
| 10.5. | Приближение многочленами высших степеней | |
| 10.6. | Квадратурная формула Гаусса | |
| 10.7. | Практическая оценка погрешности численного интегрирования | |
| 10.8. | Учет особенностей поведения подынтегральной функции | |
| 10.9. | Приближенное вычисление несобственных интегралов | |
| 10.10. | Особенности вычисления неопределенных интегралов | |
| Вопросы и задачи | ||
| Приложение. Таблица неопределенных интегралов | ||
| Список рекомендуемой литературы | ||
| Предметный указатель | ||
- Подробности
- Категория: Серия учебников "Математика в техническом университете"
Перейти к списку | Аннотация | Содержание
 Аннотация
Аннотация
Книга является седьмым выпуском комплекса учебников «Математика в техническом университете». Она знакомит читателя с кратными, криволинейными и поверхностными интегралами и с методами их вычисления. В ней уделено внимание приложениям этих типов интегралов, приведены примеры физического, механического и технического содержания. В заключительных главах изложены элементы теории поля и векторного анализа.
Содержание учебника соответствует курсу лекций, который авторы читают в МГТУ им. Н.Э. Баумана.
Для студентов технических университетов. Может быть полезен преподавателям, аспирантам и инженерам.
Содержание
| Предисловие | ||
| Основные обозначения | ||
| 1. | Двойные интегралы | |
| 1.1. | Задачи, приводящие к понятию двойного интеграла | |
| 1.2. | Определение двойного интеграла | |
| 1.3. | Условия существования двойного интеграла | |
| 1.4. | Классы интегрируемых функций | |
| 1.5. | Свойства двойного интеграла | |
| 1.6. | Теоремы о среднем значении для двойного интеграла | |
| 1.7. | Вычисление двойного интеграла | |
| 1.8. | Криволинейные координаты на плоскости | |
| 1.9. | Замена переменных в двойном интеграле | |
| 1.10. | Площадь поверхности | |
| 1.11. | Несобственные двойные интегралы | |
| Вопросы и задачи | ||
| 2. | Тройные интегралы | |
| 2.1. | Задача о вычислении массы тела | |
| 2.2. | Определение тройного интеграла | |
| 2.3. | Свойства тройного интеграла | |
| 2.4. | Вычисление тройного интеграла | |
| 2.5. | Замена переменных в тройном интеграле | |
| 2.6. | Цилиндрические и сферические координаты | |
| 2.7. | Приложения двойных и тройных интегралов | |
| Вопросы и задачи | ||
| 3. | Кратные интегралы | |
| 3.1. | Мера Жордана | |
| 3.2. | Интеграл по измеримому множеству | |
| 3.3. | Суммы Дарбу и критерии интегрируемости функции | |
| 3.4. | Свойства интегрируемых функций и кратного интеграла | |
| 3.5. | Сведение кратного интеграла к повторному | |
| 3.6. | Замена переменных в кратном интеграле | |
| 3.7. | Кратные несобственные интегралы | |
| Вопросы и задачи | ||
| 4. | Численное интегрирование | |
| 4.1. | Использование одномерных квадратурных формул | |
| 4.2. | Кубатурные формулы | |
| 4.3. | Многомерные кубатурные формулы | |
| 4.4. | Метод статистических испытаний | |
| 4.5. | Вычисление кратных интегралов методом Монте-Карло | |
| Вопросы и задачи | ||
| 5. | Криволинейные интегралы | |
| 5.1. | Криволинейный интеграл первого рода | |
| 5.2. | Вычисление криволинейного интеграла первого рода | |
| 5.3. | Механические приложения криволинейного интеграла первого рода | |
| 5.4. | Криволинейный интеграл второго рода | |
| 5.5. | Существование и вычисление криволинейного интеграла второго рода | |
| 5.6. | Свойства криволинейного интеграла второго рода | |
| 5.7. | Формула Грина | |
| 5.8. | Условия независимости криволинейного интеграла от пути интегрирования | |
| 5.9. | Вычисление криволинейного интеграла от полного дифференциала | |
| Д.5.1. | Криволинейный интеграл в многосвязной области | |
| Вопросы и задачи | ||
| 6. | Поверхностные интегралы | |
| 6.1. | О задании поверхности в пространстве | |
| 6.2. | Односторонние и двусторонние поверхности | |
| 6.3. | Площадь поверхности | |
| 6.4. | Поверхностный интеграл первого рода | |
| 6.5. | Приложения поверхностного интеграла первого рода | |
| 6.6. | Поверхностный интеграл второго рода | |
| 6.7. | Физический смысл поверхностного интеграла второго рода | |
| 6.8. | Формула Стокса | |
| 6.9. | Условия независимости криволинейного интеграла второго рода от пути интегрирования в пространстве | |
| 6.10. | Формула Остроградского - Гаусса | |
| Вопросы и задачи | ||
| 7. | Элементы теории поля | |
| 7.1. | Скалярное поле | |
| 7.2. | Градиент скалярного поля | |
| 7.3. | Векторное поле | |
| 7.4. | Векторные линии | |
| 7.5. | Поток векторного поля и дивергенция | |
| 7.6. | Циркуляция векторного поля и ротор | |
| 7.7. | Простейшие типы векторных полей | |
| Д.7.1. | Безвихревое поле в многосвязной области | |
| Д.7.2. | Векторный потенциал соленоидального поля | |
| Вопросы и задачи | ||
| 8. | Основы векторного анализа | |
| 8.1. | Оператор Гамильтона | |
| 8.2. | Свойства оператора Гамильтона | |
| 8.3. | Дифференциальные операции второго порядка | |
| 8.4. | Интегральные формулы | |
| 8.5. | Обратная задача теории поля | |
| Д.8.1. | Дифференциальные операции в ортогональных криволинейных координатах | |
| Вопросы и задачи | ||
| Список рекомендуемой литературы | ||
| Предметный указатель | ||
- Подробности
- Категория: Серия учебников "Математика в техническом университете"
Перейти к списку | Аннотация | Содержание
 Аннотация
Аннотация
Изложены основы теории обыкновенных дифференциальных уравнений (ОДУ) и даны основные понятия об уравнениях с частными производными первого порядка. Авторы стремились объединить строгость изложения теории дифференциальных уравнений с прикладной направленностью ее методов. В связи с этим приведены многочисленные примеры из механики и физики. Отдельная глава посвящена линейным ОДУ второго порядка, к которым приводят многие прикладные задачи. Главу, посвященную изложению численных методов, следует рассматривать как вводную.
Содержание учебника соответствует курсу лекций, который автор читает в МГТУ им. Н.Э. Баумана.
Для студентов технических университетов и вузов. Может быть полезен интересующимся прикладными задачами теории дифференциальных уравнений.
Содержание
| Предисловие | ||
| Основные обозначения | ||
| 1. | Общие сведения о дифференциальных уравнениях | |
| 1.1. | Основные понятия и определения | |
| 1.2. | Геометрическая интерпретация решения ОДУ. Поле направлений | |
| 1.3. | Задачи, приводящие к решению дифференциальных уравнений | |
| Вопросы и задачи | ||
| 2. | Теорема существования решения дифференциального уравнения первого порядка | |
| 2.1. | Постановка задачи Коши. Интегpальное неpавенство | |
| 2.2. | Теоpема существования и единственности pешения (теоpема Коши) | |
| 2.3. | Оценка pазности pешений двух уpавнений. Непpеpывная зависимость pешения от начальных условий и паpаметpа | |
| 2.4. | Изоклины и их использование для пpиближенного постpоения интегpальных кpивых | |
| Вопpосы и задачи | ||
| 3. | Дифференциальные уравнения первого порядка | |
| 3.1. | Диффеpенциальные уpавнения с pазделяющимися пеpеменными | |
| 3.2. | Одноpодные и квазиодноpодные уpавнения | |
| 3.3. | Уpавнения в полных диффеpенциалах. Интегpиpующий множитель | |
| 3.4. | Линейные диффеpенциальные уpавнения пеpвого поpядка. Уpавнения Беpнулли и Риккати | |
| 3.5. | Особые точки и особые решения ОДУ первого порядка | |
| 3.6. | Уpавнения, не pазpешенные относительно пpоизводной | |
| 3.7. | Особенности составления дифференциальных уравнений в прикладных задачах | |
| 3.8. | Ортогональные и изогональные траектории | |
| Вопpосы и задачи | ||
| 4. | Системы обыкновенных дифференциальных уравнений | |
| 4.1. | Задача и теоpема Коши | |
| 4.2. | Частное и общее pешения системы диффеpенциальных уpавнений | |
| 4.3. | Оценка pазности двух pешений | |
| 4.4. | Теоpема Коши о существовании и единственности pешения уpавнения высшего поpядка. Случаи понижения поpядка | |
| Вопpосы и задачи | ||
| 5. | Системы линейных дифференциальных уравнений | |
| 5.1. | Опpеделения и основные свойства pешений | |
| 5.2. | Опpеделитель Вpонского. Фундаментальная система pешений. Фоpмула Остpогpадского - Лиувилля | |
| 5.3. | Теоремы о стpуктуpе общего pешения системы ОДУ | |
| 5.4. | Метод ваpиации постоянных | |
| 5.5. | Система линейных диффеpенциальных уpавнений с постоянными коэффициентами. Хаpактеpистическое уpавнение системы | |
| 5.6. | Нахождение фундаментальной системы pешений в случае pазличных коpней хаpактеpистического уpавнения | |
| 5.7. | Стpуктуpа фундаментальной системы pешений в случае кpатных коpней | |
| Вопpосы и задачи | ||
| 6. | Линейные дифференциальные уравнения высших порядков | |
| 6.1. | Сведение к линейной системе. Опpеделитель Вpонского и стpуктуpа общего pешения одноpодного уpавнения | |
| 6.2. | Общее pешение неодноpодного уpавнения. Метод Лагpанжа ваpиации постоянных | |
| 6.3. | Понижение поpядка линейного диффеpенциального уpавнения | |
| 6.4. | Линейные дифференциальные уpавнения с постоянными коэффициентами. Случай pазличных коpней хаpактеpистического уpавнения | |
| 6.5. | Фоpмула сдвига. Случай кpатных коpней характеристического уравнения. Уpавнения Эйлеpа, Лагpанжа, Чебышева | |
| 6.6. | Стpуктуpа частного pешения уpавнения с постоянными коэффициентами и специальной пpавой частью | |
| Вопросы и задачи | ||
| 7. | Нули решений дифференциального уравнения второго порядка | |
| 7.1. | Пpиведение уpавнения к двучленному виду | |
| 7.2. | Нули pешений. Теоpема о конечности числа нулей на отpезке | |
| 7.3. | Теоpема о чеpедовании нулей. Теоремы сpавнения и Кнезеpа | |
| 7.4. | О нулях решений нелинейных дифференциальных уравнений | |
| Вопpосы и задачи | ||
| 8. | Первые интегралы | |
| 8.1. | Основные понятия и опpеделения | |
| 8.2. | Теоpема о локальном существовании системы пеpвых интегpалов | |
| 8.3. | Понижение поpядка системы диффеpенциальных уpавнений при помощи пеpвых интегpалов | |
| 8.4. | Симметричная форма записи нормальной автономной системы дифференциальных уравнений | |
| Вопpосы и задачи | ||
| 9. | Элементы теории устойчивости | |
| 9.1. | Основные опpеделения и понятия | |
| 9.2. | Устойчивость системы линейных диффеpенциальных уpавнений | |
| 9.3. | Теоpемы Ляпунова об устойчивости по пеpвому пpиближению | |
| 9.4. | Функции Ляпунова. Теоpемы Ляпунова об устойчивости и асимптотической устойчивости | |
| 9.5. | Теоpемы Четаева и Ляпунова о неустойчивости | |
| 9.6. | Библиографический комментарий | |
| Вопросы и задачи | ||
| 10. Особые точки на фазовой плоскости | ||
| 10.1. | Фазовый поpтpет системы | |
| 10.2. | Система нелинейных дифференциальных уравнений | |
| 10.3. | Математическая модель сосуществования двух популяций | |
| Вопpосы и задачи | ||
| 11. Краевые задачи для дифференциального уравнения | ||
| 11.1. | Постановка кpаевой задачи | |
| 11.2. | Линейная кpаевая задача. Сведение ее к задаче Коши | |
| 11.3. | Прикладные пpимеpы pешения кpаевой задачи | |
| Вопpосы и задачи | ||
| 12. Приближенные методы решения дифференциальных уравнений | ||
| 12.1. | Интегpиpование диффеpенциальных уpавнений при помощи степенных pядов | |
| 12.2. | Метод последовательных пpиближений | |
| 12.3. | Метод ломаных Эйлеpа | |
| 12.4. | Метод Рунге - Кутты | |
| 12.5. | Метод Чаплыгина | |
| Вопpосы и задачи | ||
| 13. Дифференциальные уравнения первого порядка с частными производными | ||
| 13.1. | Линейное дифференциальное уpавнение. Уpавнения хаpактеpистик. Задача Коши | |
| 13.2. | Квазилинейное дифференциальное уpавнение | |
| Вопpосы и задачи | ||
| Список рекомендуемой литературы | ||
| Предметный указатель | ||
- Подробности
- Категория: Серия учебников "Математика в техническом университете"
Перейти к списку | Аннотация | Содержание
 Аннотация
Аннотация
Книга является девятым выпуском комплекса учебников «Математика в техническом университете» и знакомит читателя с основными понятиями теории числовых и функциональных рядов. В книге представлены степенные ряды, ряды Тейлора, тригонометрические ряды Фурье и их приложения, а также интегралы Фурье. Изложена теория рядов в банаховых и гильбертовых пространствах, и в объеме, необходимом для ее изучения, рассмотрены вопросы функционального анализа, теории меры и интеграла Лебега. Теоретический материал сопровождается подробно разобранными примерами, рисунками и большим количеством задач разного уровня сложности.
Содержание учебника соответствует курсу лекций, который автор читает в МГТУ им. Н.Э. Баумана.
Для студентов технических университетов. Учебник может быть полезен преподавателям и аспирантам.
Содержание
| Предисловие | ||
| Основные обозначения | ||
| 1. | Числовые ряды | |
| 1.1. | Основные определения | |
| 1.2. | Необходимый признак сходимости рядов | |
| 1.3. | Свойства сходящихся рядов | |
| 1.4. | Знакоположительные ряды. Признаки сравнения | |
| 1.5. | Интегральный признак сходимости Коши | |
| 1.6. | Признак Даламбера | |
| 1.7. | Радикальный признак Коши | |
| 1.8. | Абсолютная и условная сходимости | |
| 1.9. | Знакочередующиеся ряды | |
| 1.10. | Умножение рядов | |
| 1.11. | Оценки сумм рядов | |
| Д.1.1. | Доказательство теоремы Римана об условно сходящихся рядах | |
| Д.1.2. | Признаки сходимости Дирихле и Абеля | |
| Вопросы и задачи | ||
| 2. | Функциональные ряды | |
| 2.1. | Сходимость функциональных последовательностей и рядов | |
| 2.2. | Равномерная сходимость функциональных последовательностей и рядов | |
| 2.3. | Свойства равномерно сходящихся рядов | |
| 2.4. | Комплексные степенные ряды | |
| 2.5. | Действительные степенные ряды | |
| 2.6. | Ряд Тейлора | |
| 2.7. | Разложение элементарных функций в ряд Тейлора | |
| 2.8. | Применение рядов в приближенных вычислениях | |
| 2.9. | Интегрирование обыкновенных дифференциальных уравнений с помощью рядов | |
| Д.2.1. | Остаточный член формулы Тейлора в интегральной форме | |
| Вопросы и задачи | ||
| 3. | Ряды Фурье | |
| 3.1. | Ортонормированные системы и ряды Фурье | |
| 3.2. | Комплексная форма записи тригонометрического ряда Фурье | |
| 3.3. | Ряды Фурье по тригонометрической системе | |
| 3.4. | О порядке малости коэффициентов Фурье | |
| 3.5. | Дифференцирование и интегрирование тригонометрических рядов Фурье | |
| 3.6. |
Разложение функций в тригонометрические ряды Фурье на отрезке [- |
|
| 3.7. | Сдвиг отрезка разложения | |
| 3.8. | Разложение функций в тригонометрические ряды Фурье на отрезке [ -l, l] | |
| 3.9. | Разложение четных и нечетных функций | |
| 3.10. | Разложение функций в ряды Фурье по синусам и по косинусам | |
| 3.11. | Вычисление сумм числовых рядов с помощью рядов Фурье | |
| 3.12. | Дискретное преобразование Фурье. Быстрое преобразование Фурье | |
| Д.3.1. | Доказательство леммы Римана для определенных интегралов | |
| Д.3.2. | О достаточных признаках сходимости ряда Фурье | |
| Вопросы и задачи | ||
| 4. | Интеграл Фурье | |
| 4.1. | Определение интеграла Фурье | |
| 4.2. | Представление функций интегралом Фурье | |
| 4.3. | Интеграл Фурье в случае четных и нечетных функций | |
| 4.4. | Комплексная форма интеграла Фурье | |
| 4.5. | Преобразование Фурье | |
| 4.6. | Косинус-преобразование и синус-преобразование Фурье | |
| 4.7. | Свойства преобразования Фурье | |
| Д.4.1. | Некоторые свойства несобственных интегралов с параметрами | |
| Вопросы и задачи | ||
| 5. | Ряды в нормированных пространствах | |
| 5.1. | Нормированные пространства | |
| 5.2. | Банаховы пространства | |
| 5.3. | Подпространства нормированных пространств | |
| 5.4. | Сепарабельные пространства | |
| 5.5. | Сходимость рядов в банаховых пространствах | |
| 5.6. | Банаховы пространства со счетным базисом | |
| 5.7. | Счетные базисы в пространстве непрерывных функций | |
| Д.5.1. | Неравенства Минковского и Гельдера | |
| Вопросы и задачи | ||
| 6. | Ортонормированные системы в гильбертовых пространствах | |
| 6.1. | Гильбертовы пространства | |
| 6.2. | Расстояние до подпространства | |
| 6.3. | Ортогональность | |
| 6.4. | Ортонормированные системы и ряды Фурье | |
| 6.5. | Ортонормированные базисы | |
| 6.6. | Ортогонализация и существование ортогонального базиса | |
| 6.7. | Изоморфность гильбертовых сепарабельных пространств | |
| Вопросы и задачи | ||
| 7. | Ряды по ортогональным системам в L2[a, b] | |
| 7.1. | Мера Лебега | |
| 7.2. | Измеримые функции | |
| 7.3. | Интеграл Лебега | |
| 7.4. | Банахово пространство L1[a, b] | |
| 7.5. | Гильбертово пространство L2[a, b] | |
| 7.6. | Тригонометрическая система | |
| 7.7. | Многочлены Лежандра | |
| 7.8. | Многочлены Чебышева | |
| 7.9. | Система Хаара | |
| 7.10. | Системы Радемахера и Уолша | |
| Вопросы и задачи | ||
| Список рекомендуемой литературы | ||
| Предметный указатель | ||
- Подробности
- Категория: Серия учебников "Математика в техническом университете"
Перейти к списку | Аннотация | Содержание
 Аннотация
Аннотация
Книга является десятым выпуском комплекса учебников «Математика в техническом университете» и посвящена теории функций одного комплексного переменного. В ней уделено внимание вопросам, связанным с конформными отображениями, а также применению теории к решению прикладных задач. Приведены примеры и задачи из физики, механики и разных отраслей техники.
Содержание учебника соответствует курсу лекций, который автор читает в МГТУ им. Н.Э. Баумана.
Для студентов технических университетов. Учебник может быть полезен преподавателям и аспирантам.
Содержание
| Предисловие | ||
| Основные обозначения | ||
| 1. | Комплексная плоскость | |
| 1.1. | Алгебраическая форма записи комплексного числа | |
| 1.2. | Тригонометрическая форма записи комплексного числа | |
| 1.3. | Бесконечно удаленная точка. Сфера Римана | |
| 1.4. | Геометрия на комплексной плоскости | |
| 1.5. | Задание множества точек на комплексной плоскости | |
| Вопросы и задачи | ||
| 2. | Последовательности и ряды комплексных чисел | |
| 2.1. | Последовательности комплексных чисел | |
| 2.2. | Комплексные числовые ряды | |
| 2.3. | Степенные ряды | |
| 2.4. | Круг сходимости | |
| 2.5. | Двусторонний степенной ряд | |
| Вопросы и задачи | ||
| 3. | Функции комплексного переменного | |
| 3.1. | Определение и геометрическое представление функции комплексного переменного | |
| 3.2. | Предел и непрерывность функций комплексного переменного | |
| 3.3. | Элементарные функции комплексного переменного | |
| 3.4. | Многозначная функция Arg z | |
| 3.5. | Логарифмическая функция | |
| 3.6. | Обратные тригонометрические функции | |
| Вопросы и задачи | ||
| 4. | Дифференцирование функций комплексного переменного | |
| 4.1. | Производная функции комплексного переменного | |
| 4.2. | Необходимые условия дифференцируемости | |
| 4.3. | Достаточные условия дифференцируемости | |
| 4.4. | Условия Коши - Римана в полярных координатах | |
| 4.5. | Правила дифференцирования функций комплексного переменного | |
| 4.6. | Аналитические функции | |
| 4.7. | Геометрический смысл аргумента и модуля производной | |
| 4.8. | Теорема о единственности аналитической функции | |
| 4.9. | Восстановление аналитической функции | |
| по ее действительной или мнимой части | ||
| 4.10. | Понятие об аналитическом продолжении | |
| Вопросы и задачи | ||
| 5. | Интегрирование функций комплексного переменного | |
| 5.1. | Понятие и вычисление интеграла от функции комплексного переменного | |
| 5.2. | Интегральные теоремы Коши | |
| 5.3. | Независимость интеграла от пути интегрирования | |
| 5.4. | Формула Ньютона - Лейбница | |
| 5.5. | Интегральная формула Коши | |
| 5.6. | Высшие производные аналитической функции | |
| 5.7. | Достаточные условия аналитичности функции | |
| Д.5.1. | Комплексный потенциал плоского векторного поля | |
| Вопросы и задачи | ||
| 6. | Функциональные ряды на комплексной плоскости | |
| 6.1. | Равномерная сходимость функциональных рядов | |
| 6.2. | Свойства равномерно сходящихся рядов | |
| 6.3. | Ряд Тейлора | |
| 6.4. | Разложение функций в ряд Тейлора | |
| 6.5. | Ряд Лорана | |
| 6.6. | Нахождение всевозможных разложений функции по заданным степеням | |
| 6.7. | Связь ряда Лорана с рядом Фурье | |
| Вопросы и задачи | ||
| 7. | Нули и особые точки аналитической функции | |
| 7.1. | Нули аналитической функции | |
| 7.2. | Изолированные особые точки | |
| 7.3. | Бесконечно удаленная точка как особая | |
| 7.4. | Классификация аналитических функций по их особым точкам | |
| Д.7.1. | Физическое толкование полюсов аналитической функции | |
| Вопросы и задачи | ||
| 8. | Вычеты в изолированных особых точках | |
| 8.1. | Вычет в конечной точке | |
| 8.2. | Вычисление вычета в полюсе | |
| 8.3. | Вычет в бесконечно удаленной точке | |
| 8.4. | Применение вычетов для вычисления интегралов | |
| 8.5. | Логарифмический вычет | |
| Д.8.1. | Вычисление интегралов от действительных функций | |
| Вопросы и задачи | ||
| 9. | Геометрические принципы теории функций комплексного переменного | |
| 9.1. | Взаимно однозначные отображения | |
| 9.2. | Свойства конформных отображений | |
| 9.3. | Теорема Римана | |
| 9.4. | Принцип соответствия границ | |
| 9.5. | Принцип максимума модуля функции | |
| 9.6. | Принцип симметрии | |
| Вопросы и задачи | ||
| 10. Конформные отображения | ||
| 10.1. | Линейное отображение | |
| 10.2. | Дробно-линейное отображение | |
| 10.3. | Целая степенная функция | |
| 10.4. | Показательная функция | |
| 10.5. | Функция Жуковского | |
| 10.6. | Тригонометрические и гиперболические функции | |
| 10.7. | Однозначные ветви многозначных обратных функций | |
| Д.10.1. | Отображение полуплоскости на внутренность прямоугольника | |
| Д.10.2. | Интеграл Кристоффеля - Шварца | |
| Вопросы и задачи | ||
| 11. Прикладные задачи | ||
| 11.1. | Предварительные замечания | |
| 11.2. | Непосредственное использование известного комплексного потенциала | |
| 11.3. | Обтекание цилиндрического тела | |
| 11.4. | Течение жидкости в каналах | |
| 11.5. | Задачи различного физического содержания | |
| Список рекомендуемой литературы | ||
| Предметный указатель | ||



