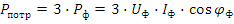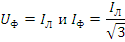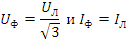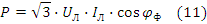Глава 3. Трехфазные системы.
Содержание главы:
3.1. Общие положения.
Электроэнергию при переменном синусоидальном напряжении можно передавать как в однофазной системе, требующей двух проводов, так и в многофазных системах. По сравнению с однофазными они имеют ряд преимуществ, но более громоздкие. Практическое распространение получила трёхфазная система переменного синусоидального напряжения. Трёхфазной системой называется совокупность электрических цепей, в ветвях которых действуют три одинаковых по амплитуде синусоидальных электродвижущих сил одинаковой частоты, с фазовыми углами одна относительно другой 120°. Одной из ЭДС присвоена литера A, следующей за ней по фазе - литера B и далее – литера C:
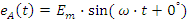
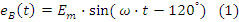
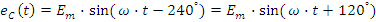
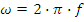 при частоте f=50 или 60 Гц.
В производстве и передаче электрической энергии трёхфазная система наиболее экономична. В ней обеспечивается сравнительно простое получение вращающегося магнитного поля, используемого в большинстве двигателей переменного напряжения. Достаточно экономично решается задача преобразования переменного напряжения в постоянное. Однофазные потребители подключаются к трёхфазной сети без существенных ограничений. В настоящее время производство электрической энергии на электростанциях, передача и распределение энергии потребителям осуществляется в единых трехфазных системах-сетях. Они распространены на значительных территориях одного или нескольких государств. Такой системой является Единая энергетическая система России. Частота напряжения в ней 50 Гц. Более сложные многофазовые системы применяются в некоторых специализированных установках.
при частоте f=50 или 60 Гц.
В производстве и передаче электрической энергии трёхфазная система наиболее экономична. В ней обеспечивается сравнительно простое получение вращающегося магнитного поля, используемого в большинстве двигателей переменного напряжения. Достаточно экономично решается задача преобразования переменного напряжения в постоянное. Однофазные потребители подключаются к трёхфазной сети без существенных ограничений. В настоящее время производство электрической энергии на электростанциях, передача и распределение энергии потребителям осуществляется в единых трехфазных системах-сетях. Они распространены на значительных территориях одного или нескольких государств. Такой системой является Единая энергетическая система России. Частота напряжения в ней 50 Гц. Более сложные многофазовые системы применяются в некоторых специализированных установках.
3.2. Источники электрической энергии.
В генераторах электрических станций система трёхфазных ЭДС образуется в одинаковых обмотках, геометрические оси которых пространственно расположены под углом 120°. Они находятся в магнитном поле вращающегося ротора. В обмотках возникает ЭДС по уравнениям (1). Следует отметить, что при описании трёхфазных цепей термин “фаза” применяется в различном смысловом значении. Это наименование каждой из обмоток генератора (трансформатора). Это так же наименование одного или группы однофазных потребителей, подключенных к линиям электропередачи. В то же время - это фазовый угол в синусоидальной функции. В общем случае трёхфазная система напряжений сети представлена потребителю в четырех проводах рис. 3.1а:
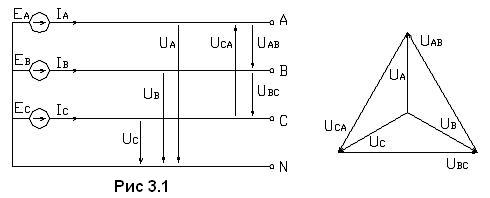
Токи в линейных проводах и напряжения между ними называются линейными. Это линейные напряжения сети UАВ, UВС, UСА. Фазные напряжения сети обозначаются UА, UВ, UС - это напряжения, определяемые фазами источника. Все напряжения и токи учитываются в действующих значениях. Синусоидальные функции фазных напряжений равны по амплитуде и имеют взаимный фазовый угол 120° в той же последовательности чередования фаз, как и ЭДС. Фазные напряжения могут быть представлены как соответствующие векторы UA, UB, UC. При этом вектор UA, которому присвоен нулевой фазовый угол, принято изображать вертикально рис. 3.1б. Связь линейных и фазных напряжений между собой устанавливается уравнениями на основе второго закона Кирхгoфа:
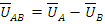
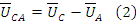
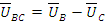
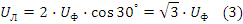
3.3. Потребители электрической энергии.
Потребителями в трёхфазных сетях могут быть однофазные и трехфазные устройства. Однофазные устройства, как правило, мало - мощные. Это устройства освещения, мало - мощные нагревательные устройства и микродвигатели, блоки питания управляющих автоматов, устройства информационных технологий - персональные компьютеры, принтеры и др. В паспорте однофазных потребителей указывается номинальное напряжение Uном. В соответствии со значением этого параметра однофазные потребители подключаются на равное ему линейное или фазное напряжение сети. Для сети это несимметричная нагрузка. Трёхфазные потребители – это электродвигатели, мощные нагревательные устройства и другие силовые установки. Они имеют три конструктивно оформленные фазы потребителя, которые идентичны. Как правило, трёхфазные устройства характеризуются достаточно большой мощностью. В паспорте трёхфазных потребителей указывается номинальное напряжение Uном - линейное. К трехфазной сети трехфазные потребители подключаются к линейным проводам.Uном = UЛ сети. При этом их фазы могут быть соединены треугольником либо звездой. Нагрузка для сети симметричная. При проектировании сети питания большого числа однофазных потребителей они группируются в фазы потребителя с примерно одинаковым количеством единичных потребителей в каждой фазе. Несимметрия нагрузки для сети уменьшается, но в общем случае сохраняется.
3.4. Соединение треугольником.
При соединении фаз потребителя треугольником каждая из фаз подключается на рис. 3.2:
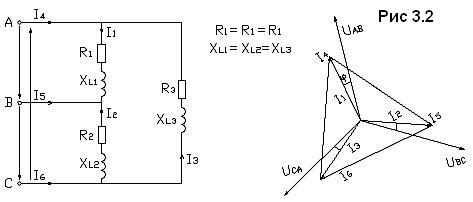
В схеме фазы потребители имеют активно-индуктивный характер. Нагрузка симметричная. Для расчета токов параметры сопротивления фаз должны быть заданы. Назначаются положительные направления токов. Линейных токов от источника сети к потребителю, фазных токов - по направлению приложенных к фазам потребителя напряжений сети. Соотношения для расчета фазных токов соединения треугольником:
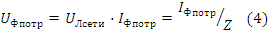
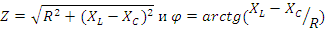
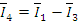
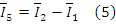
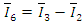
Расчет токов для соединения треугольником при симметричной нагрузке приведен в примере (4). При несимметричной нагрузке аналитический расчёт токов следует выполнять символическим методом. Справедливы общие правила составления уравнений. Необходимо рассчитать шесть токов. Схема имеет четыре узла: три в соединении треугольником и один в источнике. Независимые уравнения по первому закону Кирхгофа соответствуют уравнениям (5). Уравнения, составленные по второму закону Кирхгофа, включающие линейные напряжения и разрешённые относительно тока - это три уравнения, соответствующие уравнениям (4). Расчёт приведён в примере (5).
3.5. Соединение звездой.
При соединении фаз потребителя звездой, один из проводов каждой фазы подключается к точкам А, В, С соответственно, а остальные три провода объединяются и присоединяются к точке N. Схема соединения приведена на рис. 3.3а. При таком соединении к каждой из фаз потребителя приложено фазное напряжение сети.
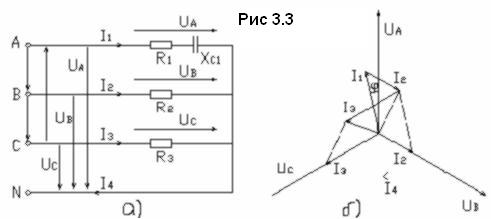
Соотношения для расчёта токов соединения звездой:
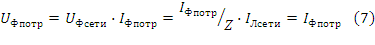
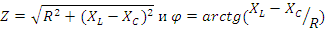
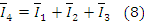
При симметрической нагрузке Z и φ каждой из фаз потребителя одинаковы. В этом случае фазные токи равны и имеют взаимный фазовый угол 120°. Их векторная сумма определяет нулевое значение тока в нейтральном проводе. Поэтому трёхфазные потребители при соединении фаз звездой к нейтральной точке не подключаются. Равенство фазных напряжений потребителя и их взаимные фазовые углы 120° обеспечиваются симметричностью нагрузки. Более сложные варианты подключения несимметричных потребителей к трёхфазной сети сводятся к схемам соединения треугольником или звездой. Они могут быть и с неполным количеством фаз. Расчёты токов и напряжений на основе графических построений векторов в векторных диаграммах возможен. Общим же случаем расчета является применение символического метода. Расчет приведён в примере (8).
3.6. Мощности в трёхфазной системе.
Определяющим при расчёте мощностей в электрических цепях является уравнение баланса мощности. Оно является выражением закона сохранения энергии. В переменных синусоидальных токах это баланс полной мощности. Он записывается по составляющим: равенству активной и реактивной мощностей источников и потребителей. Общий случай расчёта полной мощности трёхфазной сети как источника может быть выполнен символическим методом. Для каждого из фазных напряжений сети его положительное направление и положительное направление линейного тока противоположны. Значит каждое из фазных напряжений сети - источник. Уравнение расчёта полной мощности сети как источника:
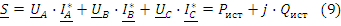
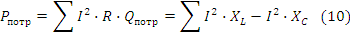
Баланс заключается в равенстве 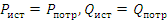 . Расчет баланса мощности указан в примере (9). При симметричной нагрузке применяются более простые выражения мощности в действительных числах. Независимо от соединения треугольником или звездой суммарная мощность для трёх фаз потребителя равна:
. Расчет баланса мощности указан в примере (9). При симметричной нагрузке применяются более простые выражения мощности в действительных числах. Независимо от соединения треугольником или звездой суммарная мощность для трёх фаз потребителя равна: